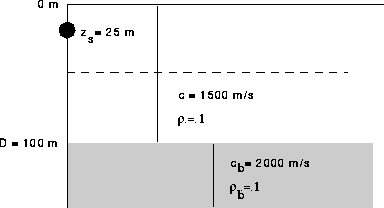
Figure: Schematic of the Pekeris problem.
The derivation of the modal equation which was followed in Sect. 2.2 is inapplicable in many ocean acoustic problems. The key assumption was that after applying the separation of variables we obtained a Sturm-Liouville problem which was non-singular and therefore possessed a complete set of normal modes. As we shall see, even fairly simple scenarios can lead to singular problems for which the normal modes do not form a complete set. More generally, one obtains a mixed spectrum composed of a discrete and a continuous part. The discrete spectrum in such cases leads to a representation involving a sum of modes while the continuous spectrum involves an integral over a continuum of points in k-space.
A simple example of such a problem is provided by the Pekeris waveguide which consists of an isovelocity layer over an isovelocity halfspace. We shall consider the particular problem shown schematically in Fig. 2.6.

Figure: Schematic of the Pekeris problem.
Applying the separation of variables technique to this problem we
obtain the modal equation (![]() ) but with the bottom depth D
going to infinity: the modal equation is singular. We can make the
domain finite by constructing a boundary condition to be applied at
the interface between the two layers. To construct the equivalent
boundary condition, we observe that the general solution in the
halfspace is given by,
) but with the bottom depth D
going to infinity: the modal equation is singular. We can make the
domain finite by constructing a boundary condition to be applied at
the interface between the two layers. To construct the equivalent
boundary condition, we observe that the general solution in the
halfspace is given by,
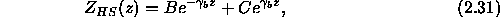
where,
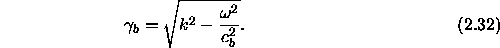
and 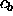 denotes the sound speed in the bottom. Let us assume for
the moment that
denotes the sound speed in the bottom. Let us assume for
the moment that 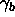 is positive. Then, in order to have a
bounded solution at infinity, we require C to vanish. At the
interface, we require continuity of pressure and normal velocity:
is positive. Then, in order to have a
bounded solution at infinity, we require C to vanish. At the
interface, we require continuity of pressure and normal velocity:
where  and
and  denote the density in the water and bottom
respectively. Dividing these two equations we find that
denote the density in the water and bottom
respectively. Dividing these two equations we find that
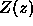 must satisfy the boundary condition
must satisfy the boundary condition
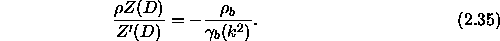
Our modal problem then reads:
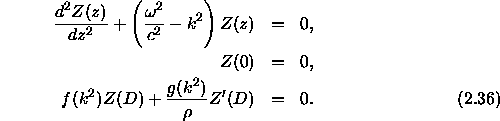
where,
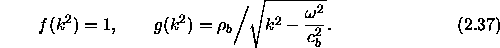
Now we have a modal problem defined on a finite domain, but the
boundary condition involves the eigenvalue 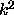 . Furthermore, the
eigenvalue enters through a square root function which introduces a
branch cut in the k-plane. Thus, we can convert a modal problem from
an infinite domain to a finite domain but the problem remains singular
and we are not assured of the completeness of the eigenfunctions.
. Furthermore, the
eigenvalue enters through a square root function which introduces a
branch cut in the k-plane. Thus, we can convert a modal problem from
an infinite domain to a finite domain but the problem remains singular
and we are not assured of the completeness of the eigenfunctions.
We shall take another tack which, briefly stated, is to take the spectral integral representation of the solution; close the contour; and calculate the integral as a sum of residues. The terms due to the residues will turn out to correspond to the modes of the problem. Thus, we start with the spectral integral representation[50]
where, 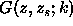 satisfies:
satisfies:
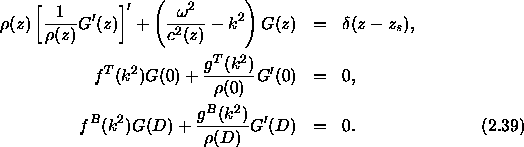
and primes denote differentiation with respect to z. The top
and bottom boundary
conditions involve functions 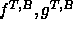 representing an
angle-dependent impedance. Incidentally, this form allows for fairly
complicated bottom types. For instance, Ref. [15]
shows how to construct an impedance condition equivalent to an
elastic subbottom.
representing an
angle-dependent impedance. Incidentally, this form allows for fairly
complicated bottom types. For instance, Ref. [15]
shows how to construct an impedance condition equivalent to an
elastic subbottom.
We shall write this problem symbolically as,
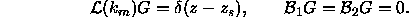
The solution of this boundary value problem is given in standard texts (e.g. Ref. [41]) as:
where 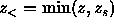 and
and 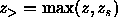 . Furthermore,
. Furthermore, 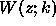 is the Wronskian:
is the Wronskian:
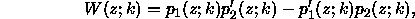
where 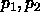 are any non-trivial solutions satisfying the top and bottom
boundary conditions respectively. That is,
are any non-trivial solutions satisfying the top and bottom
boundary conditions respectively. That is,
Let us consider a problem such as the Pekeris
waveguide which, has a single branch cut from a lower halfspace
boundary condition. We next close the contour in the spectral
integral representation by adding the semicircle  and the branch
cut integral
and the branch
cut integral  as shown in Fig. 2.7. (This particular choice
of the branch cut which follows the axes is called the EJP cut after
Ewing, Jardetsky and Press[42]). Then from Cauchy's
integral formula we can write the integral as a sum of residues:
as shown in Fig. 2.7. (This particular choice
of the branch cut which follows the axes is called the EJP cut after
Ewing, Jardetsky and Press[42]). Then from Cauchy's
integral formula we can write the integral as a sum of residues:
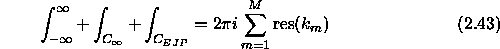
where 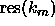 denotes the residue of the mth pole which
is enclosed by the contour. These poles are indicated schematically
by the filled circles in Fig. 2.7. (Their precise positions depend on
the frequency and parameters of the waveguide.) Additional
poles, which are not enclosed, will also occur as indicated by
the hollow circles.
Furthermore, depending on the particular problem and the choice of
the branch cut, the number of such residues may be zero, finite or
infinite.
denotes the residue of the mth pole which
is enclosed by the contour. These poles are indicated schematically
by the filled circles in Fig. 2.7. (Their precise positions depend on
the frequency and parameters of the waveguide.) Additional
poles, which are not enclosed, will also occur as indicated by
the hollow circles.
Furthermore, depending on the particular problem and the choice of
the branch cut, the number of such residues may be zero, finite or
infinite.
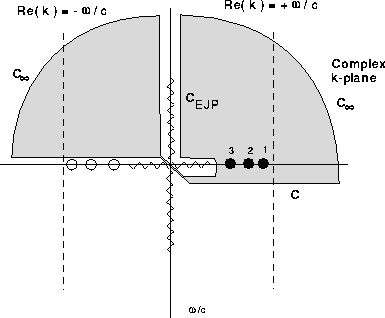
Figure: Location of eigenvalues for the Pekeris problem (EJP branch cut).
As the radius of the semicircle 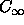 goes to infinity, the
contribution of that contour goes to zero because the Hankel function
decays exponentially as the radius increases. Substituting the
representation of the Green's function given in Eq. (
goes to infinity, the
contribution of that contour goes to zero because the Hankel function
decays exponentially as the radius increases. Substituting the
representation of the Green's function given in Eq. (![]() )
into Eq. (
)
into Eq. (![]() ) we then obtain a representation of the
field as a sum of residues plus a branch-cut integral, viz.:
) we then obtain a representation of the
field as a sum of residues plus a branch-cut integral, viz.:
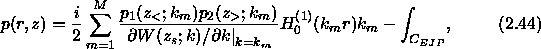
where, 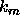 is the mth zero of the Wronskian. We arbitrarily
order these zeros so that
is the mth zero of the Wronskian. We arbitrarily
order these zeros so that 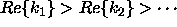 .
The equation defining the eigenvalues (
.
The equation defining the eigenvalues (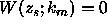 ) is known
as the
characteristic equation or secular equation. (In general, any
equation whose roots are the eigenvalues will be called a
characteristic equation.)
) is known
as the
characteristic equation or secular equation. (In general, any
equation whose roots are the eigenvalues will be called a
characteristic equation.)
Now if 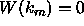 then
then 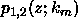 are linearly dependent and
we can simply scale them so that they are equal. We shall therefore
define
are linearly dependent and
we can simply scale them so that they are equal. We shall therefore
define
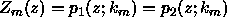 which satisfies,
which satisfies,
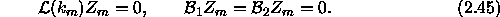
This is, of course, the standard modal equation. If 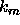 and
and 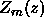 form a non-trivial solution of this modal equation, then
form a non-trivial solution of this modal equation, then 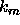 is a
zero of the Wronskian and vice versa. In terms of
is a
zero of the Wronskian and vice versa. In terms of 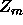 we can write
we can write
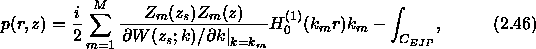
This representation of the pressure field is somewhat inconvenient
since it requires the evaluation of 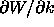 which is
defined in terms of functions
which is
defined in terms of functions 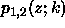 that may not be readily
available in a particular numerical scheme. In order to simplify
this expression, we seek an alternate form for
that may not be readily
available in a particular numerical scheme. In order to simplify
this expression, we seek an alternate form for 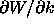 . The following result is derived in the next subsection:
. The following result is derived in the next subsection:
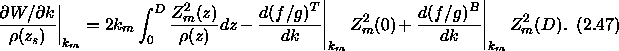
By properly scaling 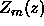 we can make
we can make
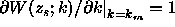 .
Thus we obtain our final representation for the pressure field
as
.
Thus we obtain our final representation for the pressure field
as
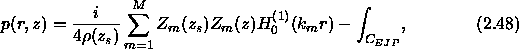
where the modes are normalized such that
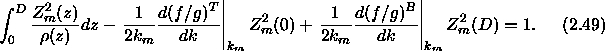
(An alternate derivation of this result is given by Bucker[43] for the constant density problem.)
It appears we have only made the problem more complicated since we have converted the original spectral integral form to one involving a sum of modes plus another integral term. In practice, however, the branch cut integral can generally be neglected if we are sufficiently far from the source.
The particular nature of the boundary conditions is important in determining the representation. As we have seen, if the upper boundary is a pressure release boundary and the lower boundary is perfectly rigid, then there are no branch-cut contributions: the solution is represented entirely as an infinite sum of modes. In problems with an elastic halfspace, there will be branch-cut terms associated with both S- and P-wave velocities in the halfspace.
Furthermore, the number of terms in the residue series depends on the particular branch cut taken. For instance, if we take the Pekeris branch-cut shown in Fig. 2.8 then it turns out that an additional (typically infinite) set of poles is exposed. These poles are represented by the filled circles numbers 4--6 in the figure. The poles in this second set lie off the real axis in the first quadrant and as a result decay exponentially in range. For this reason the corresponding modes are referred to as leaky modes. Thus, we can obtain an infinite variety of representations of the field depending on the choice of branch cut.
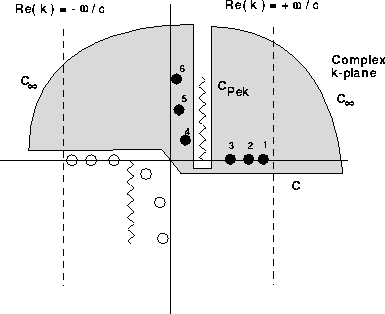
Figure: Location of eigenvalues for the Pekeris problem
(Pekeris branch cut).
In principle, the Pekeris cut offers an advantage in exposing the leaky modes for, as we shall see in the next section, by including the leaky modes we can obtain a solution which is more accurate in the near field. In practice, it is somewhat difficult to reliably locate the leaky modes so the potential gain may come at the expense of robustness in the model. In addition, the leaky modes grow exponentially in depth and at some ranges and depths yield a diverging series. Alternatively, it is also possible to calculate the branch cut term numerically as discussed by Stickler [11].
In order to clarify some of these points, let us return to the Pekeris waveguide problem. The solution in the ocean layer which satisfies the pressure release surface condition is given by
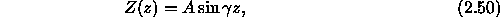
where,
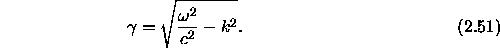
In order to obtain a non-trivial solution that satisfies the bottom boundary conditions we must have
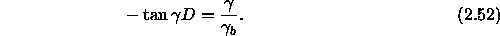
This is a transcendental equation for the eigenvalues 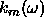 .
.
In Fig. 2.9 we have plotted selected modes of the Pekeris problem. We see that modes 1 and 4 are qualitatively similar to the previous isovelocity problem: the solution in the water column is again a sinusoid however the vertical wavenumber is different due to the change in phase associated with the bottom reflection coefficient. Also plotted in Fig. 2.9 are modes 10 and 12 which are leaky modes and therefore manifest a non-zero imaginary part as shown by the dashed line.
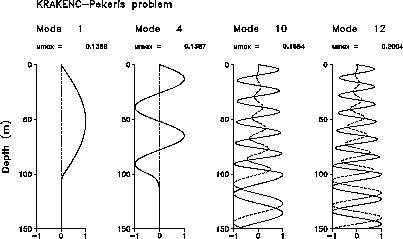
Figure: Selected modes of the Pekeris problem.
Neglecting the cylindrical spreading term, the contribution of an individual mode to the pressure field is proportional to
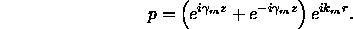
Thus, the modes can be thought of as consisting of an up and
downgoing plane-wave with an angle of propagation 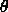 defined by
defined by
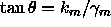 . The branch point occurs at
. The branch point occurs at 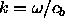 which in the angle domain corresponds precisely to the critical
angle. Thus, the modes whose angles are less than the critical angle
are trapped, that is, radiate no energy into the halfspace. The
leaky modes however have angles above the critical angle and lose
energy into the lower halfspace.
which in the angle domain corresponds precisely to the critical
angle. Thus, the modes whose angles are less than the critical angle
are trapped, that is, radiate no energy into the halfspace. The
leaky modes however have angles above the critical angle and lose
energy into the lower halfspace.