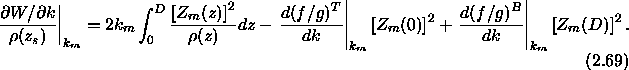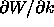In the previous section we used an expression for
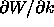necessary for
normalizing the modes which for completeness we shall now derive.
We consider the problem:
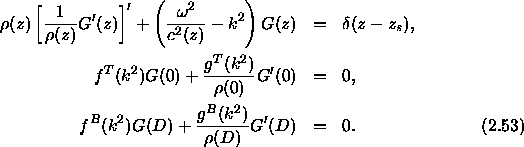
where primes denote differentiation with respect to z. We shall write this problem symbolically as,
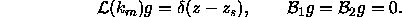
The Wronskian is defined by:
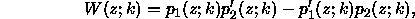
where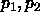 
are any non-trivial solutions that satisfy the top and bottom
boundary conditions respectively. That is,
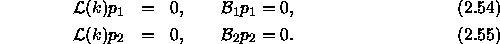
Let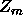 
be a solution of the unforced boundary value problem,
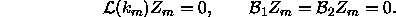
Then,
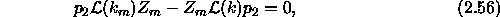
or, equivalently,
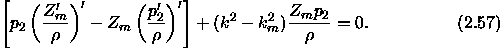
This can also be written:
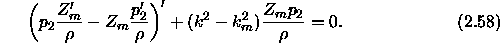
Taking the integral then gives:
We shall need two intermediate results giving the value of the term
in square brackets at z=0 and z=D. To obtain the value at z=0 we
note that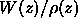 
is
constant since,
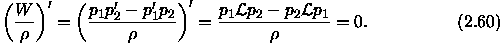
Thus, we can write:
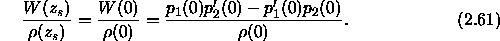
and solving for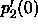 
one obtains,
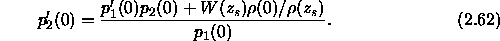
This enables us to write,
We can eliminate the derivatives from this equation using the upper boundary condition:
Thus Eq. (
) becomes:
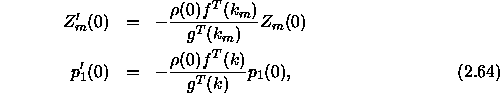
This gives us the value of the term in square brackets in Eq. ()
evaluated at z=0.
The value at z=D is can be written down directly as:
where we have used the bottom boundary condition,
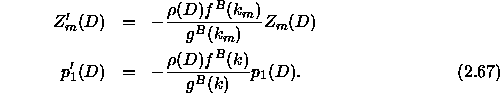
Using the results of Eqs. () and () in
Eq. () we obtain,
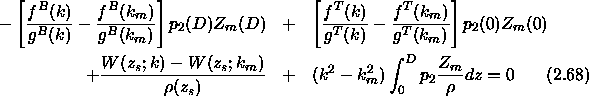
where we have added in the term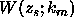 
. This is permissible since
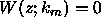, that is, the Wronskian vanishes when k is an eigenvalue.
The functions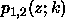 
and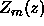 
may all be scaled freely
and still satisfy their respective governing equations. Therefore,
without loss of generality, we take 
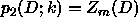. Now, dividing
both sides of the equation by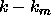 
and taking the limit as 
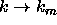we obtain the final result:
