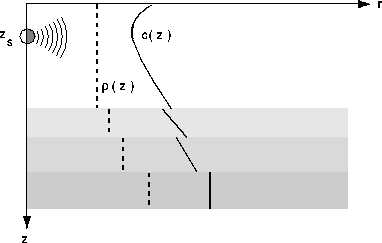
Figure: Schematic of the range-independent environmental scenario.
The problem we consider is that of calculating the response to an isotropic point source in a stratified (i.e. range-independent) acoustic medium. The scenario is indicated schematically in Fig. 2.1. Within a layer the solution is governed by the acoustic wave equation:
where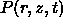 
is the acoustic pressure as a function of depth z,
range r, and time t. In addition,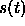 
is the isotropic point
source,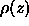 
is the density and 
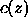is the sound speed.
For the moment we assume that the surface is a pressure release boundary
and that at some sufficiently great depth D, the boundary can be treated
as perfectly rigid:
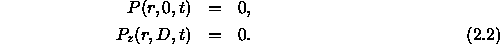
(The perfectly rigid boundary is often used as a first approximation to the ocean bottom, but in fact a pressure-release bottom is almost always a better approximation: long range propagation is dominated by rays at grazing incidence where even a relatively fast bottom acts like a pressure release boundary.) Furthermore, we require
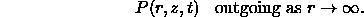
When discontinuous interfaces are present the wave equation applies within each smooth layer and interface conditions requiring continuity of pressure and normal displacement are imposed.
The first simplification we make is to assume that we are only interested in a single frequency component, that is, the response of the ocean to a continuous hum. Thus, we assume that the source time series has the form
which leads to a pressure field with the same harmonic time-dependence
:
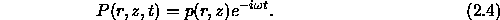
Making this substitution in the wave equation yields the so-called Helmholtz equation or reduced wave-equation:
Using the technique of separation of variables, we seek a
solution of the unforced equation (with the source removed) in the
form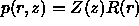 
.
Thus we find,
The two components in square brackets are functions of r and z
respectively. Thus, the only way the equation can be satisfied is if
each component is equal to a constant. Denoting this separation
constant by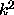 
we obtain the modal equation:
The modal equation is a classical Sturm-Liouville eigenvalue problem
whose properties are well-known[28]. (We assume for the moment that
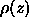and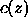 
are real functions.) A brief summary of these
properties follows. The modal equation has an infinite number of
solutions (modes) which
are characterized by a mode shape function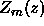 
and a horizontal
propagation constant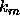 
. These horizontal propagation constants,
are all distinct.
The function 
is an eigenfunction and 
or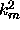 
is an
eigenvalue. The mth mode has m zeroes in the interval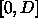 
and the
corresponding eigenvalues,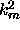 
are all real and we choose to order them
such that
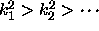. One can also show that all the
eigenvalues are less than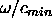 
where
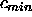is the lowest sound speed in the problem.
In addition, the modes of such Sturm-Liouville problems are orthogonal. That is,
The solutions of the modal equation are arbitrary to a multiplicative
constant as is easily seen from Eq. (
). In order to
simplify certain results, we shall assume that the modes are scaled
(normalized) so that
With this scaling, the modes form an ortho normal set. Furthermore, the set is complete which means we can represent an arbitrary function as a sum of the normal modes. Thus, we write the pressure as
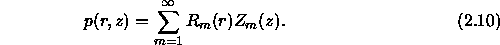
If we now substitute this into Eq. () we obtain:
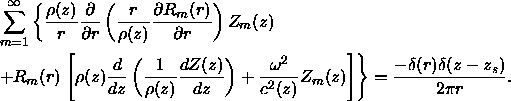
This implies,
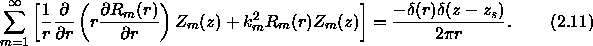
Next we apply the operator:
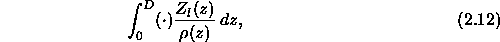
to this equation. Because of the orthogonality property (Eq. )
only the nth term in the sum remains. This gives us:
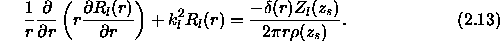
This is a standard equation whose solution is given in terms of a Hankel function[28] as
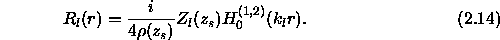
The choice of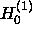 
or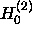 
is determined by the
radiation condition (that energy should be radiating outward as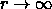 
).
Since we have suppressed a time-dependence of
the form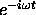 
with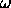 
positive and since the
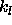are chosen to lie in the right-half plane
we shall take the Hankel function of the first kind.
Putting this all together, one finds that,
or, using the asymptotic approximation to the Hankel function,
We normally plot not the complex pressure field but transmission loss. Transmission loss is defined by:
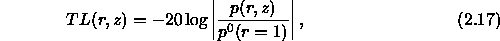
where
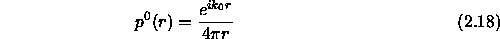
is the pressure for the source in free space. Thus one may write:
In some cases it is useful to calculate an incoherent transmission loss defined by:
If one is comparing to measured data which has been taken by averaging over frequency one can often simulate the resulting smoothed result by an incoherent TL calculation. Incoherent transmission loss is also often appropriate for shallow water problems. In shallow water the modes are normally bottom-interacting and bottom properties are usually poorly known. This in turn means that the detailed interference pattern predicted by a coherent TL calculation is not physically meaningful.
