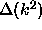The philosophy of the deflation method is to start above the first eigenvalue and use the secant method to find the first eigenvalue. Once that eigenvalue is located it is deflated, that is, divided out of the characteristic equation, and the process is repeated for each eigenvalue in turn. Interestingly, one may formally prove that the secant method will always converge to the first eigenvalue if started at a point above that first eigenvalue. (See Wilkinson, [62].) Naturally, there are some footnotes to this sweeping statement. The key one is that the characteristic function should be a polynomial. Some care is required to avoid violating this requirement. Secondly, the eigenvalues should all be real. In practice, the deflation procedure works very well for most realistic ocean acoustic problems--- even for complex eigenvalues. However, if branch cuts are present, problems are not unlikely.
The deflation of previous eigenvalues is a trivial process. Instead of
computing the characteristic function,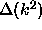 
, one computes:
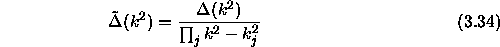
where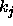 
are the previously computed eigenvalues which are to be
removed or deflated.