The solution of the above matrix eigenvalue problem proceeds in two steps. First, the eigenvalues are found by applying a root finder to the characteristic equation,
where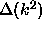 
denotes the determinant of the matrix. Finally,
once the eigenvalues are found, the eigenvectors are computed using
inverse iteration. The inverse iteration is given by,
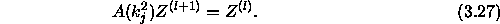
The matrix A is (nearly) singular because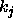 
is (nearly) an
eigenvalue of A. One may easily show that the effect of this
iteration is to continually amplify the eigenvector component in the
starting vector that corresponds to the eigenvalue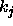 
.
Thus, the starting vector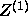 
may be picked fairly arbitrarily.
After each iteration, the new iterate 
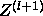is renormalized to
avoid overflow. In addition, the growth of the iterates is used as a
check for convergence. (Typically 2 iterations are sufficient.)
This inverse iteration technique is described in numerous texts on algebraic eigenvalue problems, see for instance, Wilkinson [62]. The usual development applies for this nonlinear eigenvalue problem with some minor restrictions. In particular, the inverse iteration will not be reliable in cases where one-sided shooting would be unstable for constructing the impedance conditions. There are two cases where this could be an issue: 1) when the `internal reflection coefficient' option is used recklessly and 2) for certain elastic problems with internal ducts.
One of the most difficult aspects of normal mode computations is that of finding the roots of the characteristic equation. The fundamental difficulty is that many familiar root-finding algorithms (such as the secant method or Newton's method) will only converge to a particular root if an initial guess is provided which is sufficiently close. Unfortunately, even though the eigenvalues of a purely acoustic problem are guaranteed to be distinct, they can be very nearly degenerate. As a result, many existing mode codes provide accurate but incomplete mode sets.
Two root-finding techniques are used in the KRAKEN program which we shall describe next. The first is efficient and robust, in fact fool-proof, but is applicable only to purely acoustic problems, or acoustic problems with an elastic half-space. The second is less reliable but valid for problems with elastic layers.