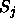For a purely acoustic problem a bisection approach is generally the most attractive solution. For this fairly broad class of problems the method will calculate a particular subset of the modes in a predictable amount of time without fail. However, for more complicated problems, for instance problems involving elasticity or complex wave speeds this technique is not applicable.
In brief, the bisection algorithm relies on the interlace property of
the Sturm-Liouville problem that the number of zeroes in a trial
eigenfunction increases monotonically as k decreases. (Recall that
the mth mode has m zeroes.) A discrete analogue of a trial
eigenfunction is the vector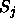 
of principal minors of A.
That is,
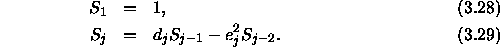
For any fixed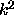 
the number of sign changes in the sequence indicates
the number of eigenvalues greater than that particular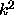 
. In
addition, the function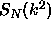 
is the characteristic equation, the
roots of which are the eigenvalues. The first property is used to
construct isolating intervals for the eigenvalues. Thus, for each
eigenvalue one computes interval endpoints which contain exactly one
eigenvalue. The second property is used by a root finder to refine the
eigenvalues within their isolating intervals.
In more detail this process proceeds as follows. First we compute an
upper bound on the eigenvalues using Gerschgorin's theorem.
(Incidentally, Gerschgorin's theorem applied to the discrete problem
yields the bound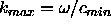 
where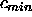 
is the
lowest sound speed in the problem.) This provides an upper bound
for the mode search. There are an infinite number of modes so that a
lower bound must be selected in some fashion. This bound is user
specified, but if it exceeds the halfspace velocity in the problem,
the bound is reduced to eliminate leaky modes from the problem.
Next, we take the midpoint of the interval and compute the number of modes to the right of the midpoint. Based on the number of zero-crossings in the trial eigenfunction one may decide whether the first eigenvalue lies to the left or to the right of the midpoint. The midpoint then becomes either a new lower bound or a new upper bound for the eigenvalue. This process of interval halving is repeated until the interval contains precisely one eigenvalue. With the isolating interval computed for the first mode, one then performs the same process for the second mode and so on. For subsequent modes an upper bound is available from the lower bound of the previous mode. In addition, information generated during the bisection for the first mode provides useful bounds for higher order modes. As a result the generation of all M of the isolating intervals typically requires little more than M bisection steps.
In the second stage these bracketing intervals are passed to sophisticated root finder (Brent's method [63]) which combines bisection, linear interpolation and inverse quadratic interpolation to provide an estimate of the eigenvalue. This latter root finder is guaranteed to converge given an isolating interval for the root. The whole process is very efficient (compared to brute force linear searching) and robust (compared to techniques which rely on asymptotic estimates to provide initial guesses for a root finder).
In practice, the sequence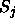 
is replaced by 
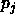where,
The sequence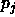 
then satisfies the following recursion:
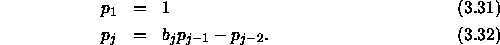
where,
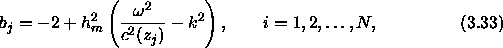
The number of sign changes in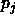 
is the same as that for the
original sequence, since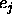 
has no sign changes. However, 
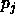is
well scaled and requires half as many floating-point operations to
compute. Incidentally, this latter sequence is precisely equivalent to
what one obtains in a simple one-sided shooting scheme. Instabilities
often occur in this sequence which are removed by simply scaling it down
as it gets too large. The scale factors are retained and passed
separately to the root finder. Surprisingly, this instability does not
in the least affect the accuracy of the eigenvalues. This is proven in
Wilkinson's text [62].
We have glossed over a difficult aspect of this method. Namely, the information provided by the Sturm sequence (regarding the number of modes to the right of some trial eigenvalue) is only justified for purely acoustic problems with free or rigid boundaries. However, for homogeneous half-spaces or elastic half-spaces there exists a simple correction to the count[16,71]. For elastic or acousto-elastic problems with more than one elastic layer or elastic gradients there is no useful extension and we are forced to use the deflation method described next.