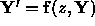 takes the form:
takes the form:
Mixed acousto-elastic problems are treated in one of two different ways.
The first approach is to simply incorporate all of the elastic effects
into a boundary condition. The particular boundary condition was
already written down in Eq. (![]() ). The coefficients of that
boundary condition require the solution of Eq. (
). The coefficients of that
boundary condition require the solution of Eq. (![]() ) which is
accomplished using a simple explicit integrator. Specifically, we
employ the modified midpoint method which for a first-order system
) which is
accomplished using a simple explicit integrator. Specifically, we
employ the modified midpoint method which for a first-order system 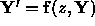 takes the form:
takes the form:
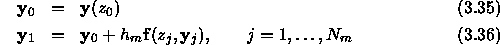
and,
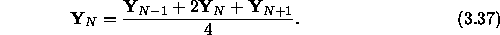
The integration is carried out in succession through each of the elastic layers to compute the coefficients of the impedance boundary condition. This approach is used in KRAKEN and KRAKENC .
The other approach, which is implemented in KRAKEL
, is simply to apply
finite differences directly to the stress-displacement equations
(![]() ). The result is a somewhat complicated 9-diagonal
matrix whose characteristic is evaluated using a LINPACK routine
(DGBDI).
). The result is a somewhat complicated 9-diagonal
matrix whose characteristic is evaluated using a LINPACK routine
(DGBDI).