As discussed in Ref. [15] the elastic quantities (stresses
and displacements)
satisfy a fourth-order system of ordinary differential equations. We
first introduce the stress-displacement vector, 
defined by
where u is the horizontal displacement, w is the vertical
displacement,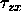 
is the tangential stress and 
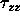is
the normal stress. The purpose of introducing the scaling of u and
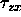given in Eq. (
) is to
eliminate complex quantities from the governing equations and to obtain
a form where the eigenvalue k occurs only in squared form. The
stress-displacement vector then satisfies
where,
where the quantities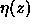 
and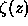 
are defined by
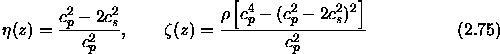
and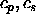 
denote the P and S wave velocities respectively. In
this form certain properties of elastic waves are immediately obvious.
For instance, since the eigenvalue occurs only as a squared quantity the
the eigenvalues will come in pairs. That is, if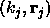 
is an
eigensolution then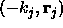 
is also an eigensolution.
The above equations for 
are combined with interfacial and
boundary conditions to completely specify the acousto-elastic modal
problem. At an elastic-elastic interface, one requires continuity of
(i.e., continuity of displacements and stresses). At an
acousto-elastic interface the condition of continuity of horizontal
displacement is relaxed. Noting that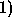 
pressure is the negative of
the normal stress,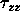 
, 
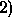
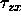vanishes in an
acoustic medium, and 
the gradient of the pressure gives the time
derivative of the velocity field, one obtains,
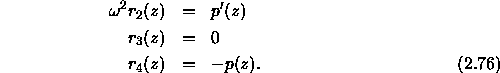
KRAKEN and KRAKENC use the reduced delta-matrix formulation. This is obtained by introducing a new set of dependent variables defined by,
where 
and 
denote two linearly independent solutions
in the elastic medium. Note that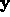 
involves all permutations of
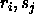with an ordering chosen to obtain a simple form for the
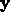equations. By differentiating the above equations and substituting
into Eq. () we find that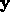 
satisfies a
system of differential equations:
where,
The differential equation for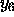 
reduces to 
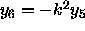and has
been eliminated from the system. In terms of the y-functions the
interface conditions between the acoustic medium and a stratified
elastic bottom can be written as,
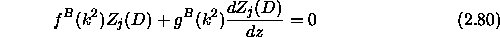
with,
