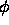 and
and 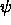 respectively. For
a bounded solution these potentials take the form:
respectively. For
a bounded solution these potentials take the form:
The solution for a homogeneous elastic medium is given in
terms of P- and S-wave potentials, 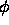 and
and 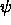 respectively. For
a bounded solution these potentials take the form:
respectively. For
a bounded solution these potentials take the form:
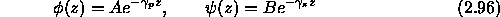
where,
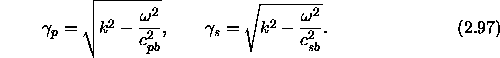
In terms of these potentials, the elastic displacements are given by,
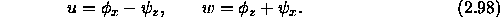
So in terms of u and w we can write the most general form of the half-space solution as:
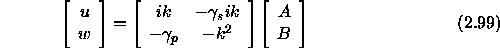
Recall,
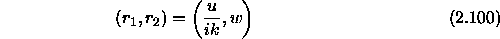
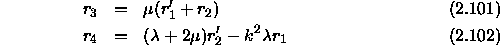
so that the most general solution in the lower half-space is
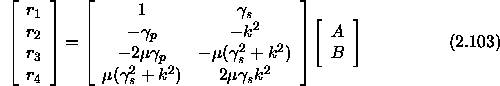
Taking the columns of the above matrix as two linearly independent
solutions and substituting into the the definitions of y
in Eq.
(![]() ) we obtain the following boundary conditions,
) we obtain the following boundary conditions,
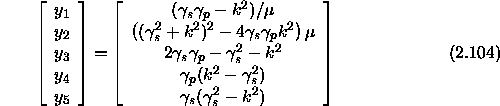
Note that the classical dispersion relation for Rayleigh waves is obtained by
taking the free surface condition 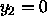 .
.