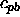 and a density,
and a density, 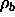 . The general solution in
the half-space is given by,
. The general solution in
the half-space is given by,
We consider first an acoustic bottom half-space characterized by a single
wave speed, 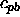 and a density,
and a density, 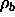 . The general solution in
the half-space is given by,
. The general solution in
the half-space is given by,
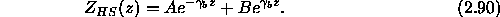
where,
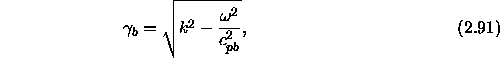
and the Pekeris branch of the square root is used to expose the leaky modes. In order to have a bounded solution at infinity, we require B to vanish. At the interface, we require continuity of pressure and normal displacement which implies,
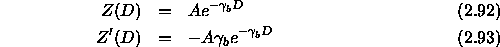
Thus, we obtain the bottom impedance condition,
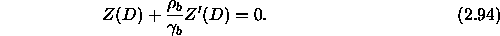
A similar procedure yields the result for a top homogeneous half-space,
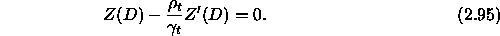
which differs by a sign change. Note that by letting 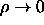 we
obtain the free-surface boundary condition and
we
obtain the free-surface boundary condition and 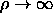 gives
the perfectly rigid boundary condition.
gives
the perfectly rigid boundary condition.