NORMAL

  
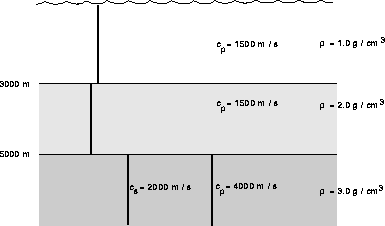
Figure: Schematic of the NORMAL problem.

Mode normalization is checked using several density changes. Due to the shear in the lower halfspace, there is a Scholte wave with a phase velocity of about 1393 m/s. It has been excluded from the calculation.

'Mode normalization test'
10.0
2
'NVF'
300 0.0 3000.0
    0.0 1500.0 /
 3000.0 1500.0 /
200 0.0 5000.0
 3000.0 1500.0    0.0 2.0 /
 5000.0 1500.0    0.0 2.0 /
'A' 0.0
 5000.0 4000.0 2000.0 3.0 /
1400.0 2000.0
1000.0                    ! RMAX (km)
1  500.0 /                ! NSD  SD(1:NSD)
1 2500.0 /                ! NRD  RD(1:NRD)

 KRAKEN- Mode normalization test
 Frequency =   10.00     NMEDIA =   2


     N2-LINEAR approximation to SSP
     Attenuation units: dB/mkHz
     VACUUM


      Z          ALPHAR     BETAR      RHO       ALPHAI     BETAI


          ( Number of pts =   300  RMS roughness =  0.000E+00 )
      0.00      1500.00      0.00     1.00       0.0000    0.0000
   3000.00      1500.00      0.00     1.00       0.0000    0.0000

          ( Number of pts =   200  RMS roughness =  0.000E+00 )
   3000.00      1500.00      0.00     2.00       0.0000    0.0000
   5000.00      1500.00      0.00     2.00       0.0000    0.0000

                                 ( RMS roughness =  0.000E+00 )
     ACOUSTO-ELASTIC half-space
   5000.00      4000.00   2000.00     3.00       0.0000    0.0000

 CLOW =   1400.0      CHIGH =   2000.0    
 RMAX =    1000.000000000000    

 Number of sources   =            1
   500.0000    

 Number of receivers =            1
   2500.000    

 Mesh multiplier   CPU seconds
        1             5.55    
        2             6.40    
        4             4.54    

    I           K                ALPHA         PHASE SPEED
    1   0.4188367900E-01   0.0000000000E+00    1500.151242    
    2   0.4186658699E-01   0.0000000000E+00    1500.763678    
    3   0.4184753177E-01   0.0000000000E+00    1501.447049    
    4   0.4180919493E-01   0.0000000000E+00    1502.823797    
    5   0.4176674150E-01   0.0000000000E+00    1504.351329    
    6   0.4171909765E-01   0.0000000000E+00    1506.069321    
    7   0.4164470397E-01   0.0000000000E+00    1508.759748    
    8   0.4158680917E-01   0.0000000000E+00    1510.860158    
    9   0.4149472381E-01   0.0000000000E+00    1514.213069    
   10   0.4140185763E-01   0.0000000000E+00    1517.609515    
   11   0.4131280307E-01   0.0000000000E+00    1520.880899    
   12   0.4117924681E-01   0.0000000000E+00    1525.813557    
   13   0.4108058576E-01   0.0000000000E+00    1529.478022    
   14   0.4093552018E-01   0.0000000000E+00    1534.898123    
   15   0.4078858493E-01   0.0000000000E+00    1540.427381    
   16   0.4065836697E-01   0.0000000000E+00    1545.360961    
   17   0.4046343001E-01   0.0000000000E+00    1552.805905    
   18   0.4032142497E-01   0.0000000000E+00    1558.274617    
   19   0.4012239980E-01   0.0000000000E+00    1566.004361    
   20   0.3991798210E-01   0.0000000000E+00    1574.023780    
   21   0.3974491332E-01   0.0000000000E+00    1580.877849    
   22   0.3948540371E-01   0.0000000000E+00    1591.267840    
   23   0.3929733220E-01   0.0000000000E+00    1598.883424    
   24   0.3904083516E-01   0.0000000000E+00    1609.388037    
   25   0.3877585468E-01   0.0000000000E+00    1620.386026    
   26   0.3855610943E-01   0.0000000000E+00    1629.621194    
   27   0.3822733064E-01   0.0000000000E+00    1643.636948    
   28   0.3799085539E-01   0.0000000000E+00    1653.867817    
   29   0.3766977091E-01   0.0000000000E+00    1667.964831    
   30   0.3734233184E-01   0.0000000000E+00    1682.590507    
   31   0.3706900744E-01   0.0000000000E+00    1694.996910    
   32   0.3666482678E-01   0.0000000000E+00    1713.681983    
   33   0.3637907870E-01   0.0000000000E+00    1727.142504    
   34   0.3598056675E-01   0.0000000000E+00    1746.271911    
   35   0.3559408137E-01   0.0000000000E+00    1765.233169    
   36   0.3525354551E-01   0.0000000000E+00    1782.284652    
   37   0.3477030998E-01   0.0000000000E+00    1807.054729    
   38   0.3443753112E-01   0.0000000000E+00    1824.516771    
   39   0.3393983898E-01   0.0000000000E+00    1851.271395    
   40   0.3351944923E-01   0.0000000000E+00    1874.489424    
   41   0.3307617837E-01   0.0000000000E+00    1899.610419    
   42   0.3254372213E-01   0.0000000000E+00    1930.690436    
   43   0.3214824698E-01   0.0000000000E+00    1954.441034    
   44   0.3155272679E-01   0.0000000000E+00    1991.328784

  
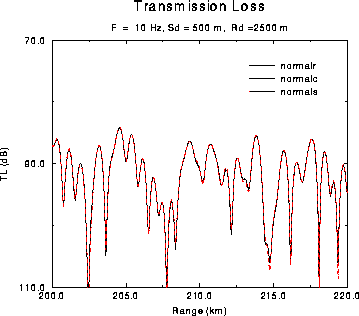
Figure: Transmission loss for the NORMAL problem.