ICE

  
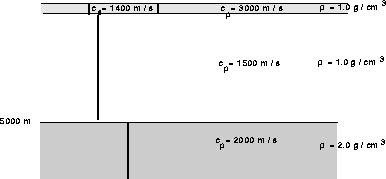
Figure: Schematic of the ICE problem.

This problem is loosely based on an Arctic scenario with an elastic ice-canopy. Here the elastic medium lies above the acoustic media. Note that the KRAKEN result disagrees with both KRAKENC and SCOOTER . This is expected since KRAKEN ignores attenuation in elastic media.

'Ice problem'
10.0
2
'NVW'
50 0.0 30.0
     0.0 3000.0 1400.0 1.0 0.3 1.0
    30.0 3000.0 1400.0 1.0 0.3 1.0 
500 0.0 5000.0
    30.0 1500.0    0.0 1.0 0.0 0.0
  5000.0 1500.0    0.0 1.0 0.0 0.0
'A' 0.0
  5000.0 2000.0    0.0 2.0 0.0 0.0
1400.0 2000.0
1000.0                    ! RMAX (km)
1  500.0 /                ! NSD  SD(1:NSD)
1 2500.0 /                ! NRD  RD(1:NRD)

 KRAKEN- Ice problem
 Frequency =   10.00     NMEDIA =   2


     N2-LINEAR approximation to SSP
     Attenuation units: dB/wavelength
     VACUUM


      Z          ALPHAR     BETAR      RHO       ALPHAI     BETAI


          ( Number of pts =    50  RMS roughness =  0.000E+00 )
      0.00      3000.00   1400.00     1.00       0.3000    1.0000
     30.00      3000.00   1400.00     1.00       0.3000    1.0000

          ( Number of pts =   500  RMS roughness =  0.000E+00 )
     30.00      1500.00      0.00     1.00       0.0000    0.0000
   5000.00      1500.00      0.00     1.00       0.0000    0.0000

                                 ( RMS roughness =  0.000E+00 )
     ACOUSTO-ELASTIC half-space
   5000.00      2000.00      0.00     2.00       0.0000    0.0000

 CLOW =   1400.0      CHIGH =   2000.0    
 RMAX =    1000.000000000000    

 Number of sources   =            1
   500.0000    

 Number of receivers =            1
   2500.000    

 Mesh multiplier   CPU seconds
        1             11.5    
        2             16.6    

    I           K                ALPHA         PHASE SPEED
    1   0.4188333139E-01   0.0000000000E+00    1500.163692    
    2   0.4186961576E-01   0.0000000000E+00    1500.655115    
    3   0.4184674417E-01   0.0000000000E+00    1501.475307    
    4   0.4181469833E-01   0.0000000000E+00    1502.626004    
    5   0.4177345263E-01   0.0000000000E+00    1504.109646    
    6   0.4172297425E-01   0.0000000000E+00    1505.929388    
    7   0.4166322309E-01   0.0000000000E+00    1508.089111    
    8   0.4159415182E-01   0.0000000000E+00    1510.593445    
    9   0.4151570588E-01   0.0000000000E+00    1513.447784    
   10   0.4142782343E-01   0.0000000000E+00    1516.658320    
   11   0.4133043533E-01   0.0000000000E+00    1520.232066    
   12   0.4122346498E-01   0.0000000000E+00    1524.176900    
   13   0.4110682824E-01   0.0000000000E+00    1528.501608    
   14   0.4098043325E-01   0.0000000000E+00    1533.215930    
   15   0.4084418017E-01   0.0000000000E+00    1538.330622    
   16   0.4069796094E-01   0.0000000000E+00    1543.857521    
   17   0.4054165894E-01   0.0000000000E+00    1549.809621    
   18   0.4037514862E-01   0.0000000000E+00    1556.201159    
   19   0.4019829503E-01   0.0000000000E+00    1563.047712    
   20   0.4001095339E-01   0.0000000000E+00    1570.366306    
   21   0.3981296844E-01   0.0000000000E+00    1578.175543    
   22   0.3960417391E-01   0.0000000000E+00    1586.495737    
   23   0.3938439178E-01   0.0000000000E+00    1595.349077    
   24   0.3915343149E-01   0.0000000000E+00    1604.759805    
   25   0.3891108916E-01   0.0000000000E+00    1614.754417    
   26   0.3865714660E-01   0.0000000000E+00    1625.361895    
   27   0.3839137032E-01   0.0000000000E+00    1636.613972    
   28   0.3811351037E-01   0.0000000000E+00    1648.545423    
   29   0.3782329915E-01   0.0000000000E+00    1661.194409    
   30   0.3752045003E-01   0.0000000000E+00    1674.602864    
   31   0.3720465592E-01   0.0000000000E+00    1688.816938    
   32   0.3687558766E-01   0.0000000000E+00    1703.887506    
   33   0.3653289237E-01   0.0000000000E+00    1719.870752    
   34   0.3617619171E-01   0.0000000000E+00    1736.828840    
   35   0.3580508009E-01   0.0000000000E+00    1754.830681    
   36   0.3541912307E-01   0.0000000000E+00    1773.952815    
   37   0.3501785613E-01   0.0000000000E+00    1794.280405    
   38   0.3460078429E-01   0.0000000000E+00    1815.908349    
   39   0.3416738384E-01   0.0000000000E+00    1838.942465    
   40   0.3371710848E-01   0.0000000000E+00    1863.500635    
   41   0.3324940638E-01   0.0000000000E+00    1889.713529    
   42   0.3276376704E-01   0.0000000000E+00    1917.723716    
   43   0.3225987273E-01   0.0000000000E+00    1947.678269    
   44   0.3173836536E-01   0.0000000000E+00    1979.681448

  
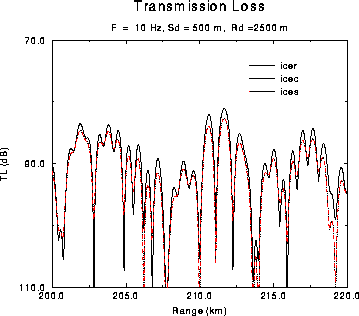
Figure: Transmission loss for the ICE problem.