DOUBLE

  
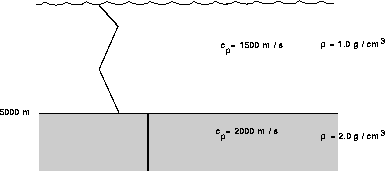
Figure: Schematic of the DOUBLE problem.

The ocean profile is converted to one involving three piecewise linear segments defining a double-duct profile.

'Double-duct problem'
10.0
3
'NVF'
100 0.0 1000.0
    0.0 1500.0 /
 1000.0 1550.0 /
200 0.0 3000.0
 1000.0 1550.0 /
 3000.0 1500.0 /
200 0.0 5000.0
 3000.0 1500.0 /
 5000.0 1550.0 /
'A' 0.0
 5000.0 2000.0   0.0 2.0 0.0 0.0
1400.0 2000.0
1000.0                    ! RMAX (km)
1  500.0 /                ! NSD  SD(1:NSD)
1 2500.0 /                ! NRD  RD(1:NRD)

 KRAKEN- Double-duct problem
 Frequency =   10.00     NMEDIA =   3


     N2-LINEAR approximation to SSP
     Attenuation units: dB/mkHz
     VACUUM


      Z          ALPHAR     BETAR      RHO       ALPHAI     BETAI


          ( Number of pts =   100  RMS roughness =  0.000E+00 )
      0.00      1500.00      0.00     1.00       0.0000    0.0000
   1000.00      1550.00      0.00     1.00       0.0000    0.0000

          ( Number of pts =   200  RMS roughness =  0.000E+00 )
   1000.00      1550.00      0.00     1.00       0.0000    0.0000
   3000.00      1500.00      0.00     1.00       0.0000    0.0000

          ( Number of pts =   200  RMS roughness =  0.000E+00 )
   3000.00      1500.00      0.00     1.00       0.0000    0.0000
   5000.00      1550.00      0.00     1.00       0.0000    0.0000

                                 ( RMS roughness =  0.000E+00 )
     ACOUSTO-ELASTIC half-space
   5000.00      2000.00      0.00     2.00       0.0000    0.0000

 CLOW =   1400.0      CHIGH =   2000.0    
 RMAX =    1000.000000000000    

 Number of sources   =            1
   500.0000    

 Number of receivers =            1
   2500.000    

 Mesh multiplier   CPU seconds
        1             5.60    
        2             6.18    

    I           K                ALPHA         PHASE SPEED
    1   0.4171018652E-01   0.0000000000E+00    1506.391084    
    2   0.4147891740E-01   0.0000000000E+00    1514.790091    
    3   0.4131862874E-01   0.0000000000E+00    1520.666464    
    4   0.4123681174E-01   0.0000000000E+00    1523.683583    
    5   0.4117017415E-01   0.0000000000E+00    1526.149801    
    6   0.4104029641E-01   0.0000000000E+00    1530.979515    
    7   0.4091561041E-01   0.0000000000E+00    1535.645013    
    8   0.4080128302E-01   0.0000000000E+00    1539.947973    
    9   0.4074949725E-01   0.0000000000E+00    1541.904988    
   10   0.4068324597E-01   0.0000000000E+00    1544.415928    
   11   0.4057281144E-01   0.0000000000E+00    1548.619650    
   12   0.4046123964E-01   0.0000000000E+00    1552.889967    
   13   0.4035440690E-01   0.0000000000E+00    1557.001029    
   14   0.4024224926E-01   0.0000000000E+00    1561.340487    
   15   0.4011172669E-01   0.0000000000E+00    1566.421051    
   16   0.3996592323E-01   0.0000000000E+00    1572.135660    
   17   0.3980769235E-01   0.0000000000E+00    1578.384713    
   18   0.3964207800E-01   0.0000000000E+00    1584.978796    
   19   0.3946677171E-01   0.0000000000E+00    1592.019067    
   20   0.3927946746E-01   0.0000000000E+00    1599.610614    
   21   0.3907987820E-01   0.0000000000E+00    1607.780166    
   22   0.3886748929E-01   0.0000000000E+00    1616.565778    
   23   0.3864545686E-01   0.0000000000E+00    1625.853546    
   24   0.3841222010E-01   0.0000000000E+00    1635.725634    
   25   0.3816711818E-01   0.0000000000E+00    1646.229951    
   26   0.3790948500E-01   0.0000000000E+00    1657.417743    
   27   0.3763853318E-01   0.0000000000E+00    1669.349142    
   28   0.3735627690E-01   0.0000000000E+00    1681.962398    
   29   0.3706135033E-01   0.0000000000E+00    1695.347107    
   30   0.3675356291E-01   0.0000000000E+00    1709.544548    
   31   0.3643204686E-01   0.0000000000E+00    1724.631430    
   32   0.3609604877E-01   0.0000000000E+00    1740.685067    
   33   0.3574683553E-01   0.0000000000E+00    1757.689937    
   34   0.3538311960E-01   0.0000000000E+00    1775.757869    
   35   0.3500480248E-01   0.0000000000E+00    1794.949511    
   36   0.3461083089E-01   0.0000000000E+00    1815.381239    
   37   0.3420046728E-01   0.0000000000E+00    1837.163585    
   38   0.3377442369E-01   0.0000000000E+00    1860.338274    
   39   0.3333144286E-01   0.0000000000E+00    1885.062502    
   40   0.3287145204E-01   0.0000000000E+00    1911.441362    
   41   0.3239342265E-01   0.0000000000E+00    1939.648482    
   42   0.3189739326E-01   0.0000000000E+00    1969.811532

  
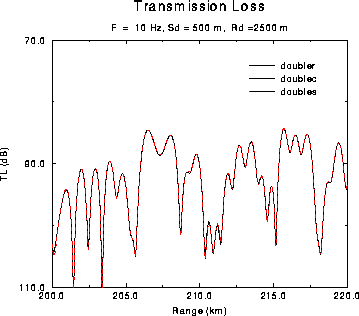
Figure: Transmission loss for the DOUBLE problem.