PEKERIS

  
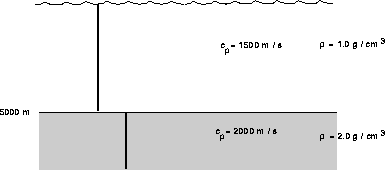
Figure: Schematic of the PEKERIS problem.

This problem involves a homogeneous fluid layer with a sound speed of 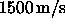overlying a faster bottom with sound speed 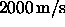and density of .

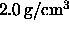'Pekeris problem'
10.0
1
'NVF'
500  0.0  5000.0
     0.0  1500.0 /
  5000.0  1500.0 /
'A'  0.0
  5000.0  2000.0  0.0  2.0 /
1400.0  2000.0
1000.0                    ! RMAX (km)
1  500.0 /                ! NSD  SD(1:NSD)
1 2500.0 /                ! NRD  RD(1:NRD)

 KRAKEN- Pekeris problem
 Frequency =   10.00     NMEDIA =   1


     N2-LINEAR approximation to SSP
     Attenuation units: dB/mkHz
     VACUUM


      Z          ALPHAR     BETAR      RHO       ALPHAI     BETAI


          ( Number of pts =   500  RMS roughness =  0.000E+00 )
      0.00      1500.00      0.00     1.00       0.0000    0.0000
   5000.00      1500.00      0.00     1.00       0.0000    0.0000

                                 ( RMS roughness =  0.000E+00 )
     ACOUSTO-ELASTIC half-space
   5000.00      2000.00      0.00     2.00       0.0000    0.0000

 CLOW =   1400.0      CHIGH =   2000.0    
 RMAX =    1000.000000000000    

 Number of sources   =            1
   500.0000    

 Number of receivers =            1
   2500.000    

 Mesh multiplier   CPU seconds
        1             5.49    
        2             6.21    

    I           K                ALPHA         PHASE SPEED
    1   0.4188332253E-01   0.0000000000E+00    1500.164010    
    2   0.4186958032E-01   0.0000000000E+00    1500.656385    
    3   0.4184666447E-01   0.0000000000E+00    1501.478167    
    4   0.4181455674E-01   0.0000000000E+00    1502.631092    
    5   0.4177323161E-01   0.0000000000E+00    1504.117605    
    6   0.4172265636E-01   0.0000000000E+00    1505.940862    
    7   0.4166279103E-01   0.0000000000E+00    1508.104751    
    8   0.4159358848E-01   0.0000000000E+00    1510.613904    
    9   0.4151499439E-01   0.0000000000E+00    1513.473722    
   10   0.4142694720E-01   0.0000000000E+00    1516.690399    
   11   0.4132937809E-01   0.0000000000E+00    1520.270954    
   12   0.4122221089E-01   0.0000000000E+00    1524.223270    
   13   0.4110536194E-01   0.0000000000E+00    1528.556132    
   14   0.4097873993E-01   0.0000000000E+00    1533.279285    
   15   0.4084224568E-01   0.0000000000E+00    1538.403485    
   16   0.4069577186E-01   0.0000000000E+00    1543.940567    
   17   0.4053920272E-01   0.0000000000E+00    1549.903522    
   18   0.4037241363E-01   0.0000000000E+00    1556.306582    
   19   0.4019527072E-01   0.0000000000E+00    1563.165317    
   20   0.4000763035E-01   0.0000000000E+00    1570.496741    
   21   0.3980933859E-01   0.0000000000E+00    1578.319442    
   22   0.3960023053E-01   0.0000000000E+00    1586.653720    
   23   0.3938012967E-01   0.0000000000E+00    1595.521741    
   24   0.3914884708E-01   0.0000000000E+00    1604.947725    
   25   0.3890618058E-01   0.0000000000E+00    1614.958141    
   26   0.3865191380E-01   0.0000000000E+00    1625.581942    
   27   0.3838581509E-01   0.0000000000E+00    1636.850824    
   28   0.3810763645E-01   0.0000000000E+00    1648.799530    
   29   0.3781711221E-01   0.0000000000E+00    1661.466183    
   30   0.3751395766E-01   0.0000000000E+00    1674.892680    
   31   0.3719786754E-01   0.0000000000E+00    1689.125136    
   32   0.3686851438E-01   0.0000000000E+00    1704.214399    
   33   0.3652554677E-01   0.0000000000E+00    1720.216633    
   34   0.3616858743E-01   0.0000000000E+00    1737.194000    
   35   0.3579723130E-01   0.0000000000E+00    1755.215440    
   36   0.3541104368E-01   0.0000000000E+00    1774.357560    
   37   0.3500955866E-01   0.0000000000E+00    1794.705659    
   38   0.3459227830E-01   0.0000000000E+00    1816.354868    
   39   0.3415867360E-01   0.0000000000E+00    1839.411384    
   40   0.3370818983E-01   0.0000000000E+00    1863.993688    
   41   0.3324026217E-01   0.0000000000E+00    1890.233379    
   42   0.3275436107E-01   0.0000000000E+00    1918.274423    
   43   0.3225014368E-01   0.0000000000E+00    1948.265834    
   44   0.3172824619E-01   0.0000000000E+00    1980.312832

  
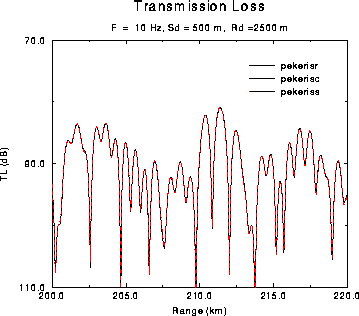
Figure: Transmission loss for the PEKERIS problem.