The full two-way coupled mode formulation allows for interactions between each segment in range and as a result leads to a global problem rather than a marching type of solution provided by, for instance, the parabolic equation. Computation time can be reduced by neglecting these multiple interactions, usually with only a minor degradation in accuracy.
An efficient marching implementation of coupled modes can be done in
several ways with different degrees of accuracy. This is discussed
in detail in Ref. [80]. A good compromise between
accuracy and complexity is provided by the single-scatter
formulation which treats each interface in range as an independent
process thus neglecting the higher-order multiple-scattering terms.
To derive this form we begin with the matching condition for the
jth interface given in Eq. (
):
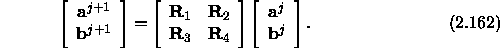
For the single-scatter approximation, the incoming wave in the left
segment is assumed to be given, and we require that the solution is purely
outgoing in the right segment, i.e.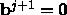 
.
Solving for the backscattered amplitudes, 
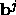, we find:
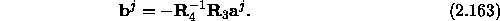
Therefore, the forward scattered amplitudes,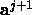 
, are given by
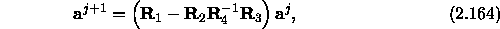
which is an explicit equation for the forward scattered field. The field in any given segment can then be computed by summing the terms in the modal sum representing the forward scattered field.
In practice, an approximate single-scatter solution works nearly as well. This solution is obtained by neglecting lower-order terms in the single-scatter recursion:
It can be shown that the matrix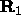 
is an arithmetic mean of
coupling matrices based on pressure matching and velocity matching.