The Twersky scatter model is used primarily for modeling under-ice scatter effects as suggested by Diachok [51]. In effect the ice is modeled as a free surface with a uniform distribution of cylindrical bosses with elliptical cross-sections which crudely represent ice keels. A reflection coefficient for this rough surface is constructed by combining the effects of the scattering function for each individual cylindrical boss. The scattering function is in turn computed analytically by a modal sum involving Mathieu functions. The program for computing this specular reflection coefficient was developed by Wales[52] for a spectral integral code.
The cylindrical bosses are described in terms of the principal radii of
the elliptical cross-section, the linear density, i.e. the number of
bosses per kilometer, and whether the bosses are perfectly free or rigid
objects. This leads to a reflection coefficient,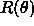 
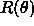, which is
a complex number incorporating both phase and amplitude information.
The reflection coefficient is formally valid in the far-field but is
applied in an ad hoc fashion at the ice/water interface. This
analytical formula for the surface reflection coefficient is then
converted to an equivalent Robin boundary condition using Eq.
(
).